엘리스에서 제공한 강의와 자료를 보고 정리한 내용입니다.

✅ 확률
확률(Probability)은 어떤 사건이 일어날 때 우리가 집중하고자 하는 사건이 어느 정도의 비율로 일어나는지를 알려준다.
같은 원인에서 특정한 결과가 나타나는 비율을 뜻하기도 한다.
우리가 일어나기를 기대하는 사건을 근원사건이라고 정의한다면 근원사건이 일어날 확률은 다음과 같다.

확률의 계산에 있어 원소란 사건이 일어남에 있어 나타날 수 있는 모든 상황을 의미한다.
경우의 수와 달리 확률은 원소가 나타나는 빈도를 고려한다.
확률은 0부터 1까지의 값을 가지며 확률값이 0이면 절대 일어나지 않는 사건, 1이면 반드시 일어나는 사건임을 의미한다.
확률은 P로 표기한다.
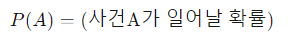
✔️ 통계적 확률
확률식을 적용하는 데 있어 중요한 점은 각각의 경우가 일어날 확률이 동일해야 한다는 점이다.
만약 주사위의 무게가 한쪽에 치우쳐져 있어 어떠한 수가 나올 가능성이 더 높다면 주사위에서 어떠한 수가 나올 확률은 1/6이 될 수 없다.
이렇듯 단순히 숫자의 계산만으로 정확한 확률을 구하지 못하는 경우가 존재한다.
통계적 확률은 이론적 확률과 달리 실제 시행을 통해 얻어진 결과를 사용한다.
큰 수의 법칙에 따라 시행횟수가 충분히 크다면 통계적 확률은 계산된 확률의 근사치로 사용될 수 있다.
✅ 독립사건과 종속사건
✔️ 독립사건
독립사건은 확률값을 구하는 데 다른 사건의 영향을 받지 않는 사건을 의미한다.
예를 들어 주사위를 두 번 던지는 경우 첫 번째에 1이 나오는 사건은 두 번째에 1이 나오는 사건에 영향을 주지 않으므로 독립사건에 해당한다.
또 다른 예로는 복원시행이 있는데 이는 주머니에서 공을 꺼낸 뒤 확인하고 다시 집어넣어 처음과 같은 조건에서 다시 공을 꺼내는 것이다.
이 경우에도 첫 번째에 흰 공을 꺼내는 사건이 두 번째에 흰 공을 꺼내는 사건에 영향을 주지 않는다.
✔️ 종속사건
종속사건은 독립사건과 반대로 어떤 사건 A와 B가 일어날 때 두 사건 사이에 영향이 존재하는 경우를 의미한다.
예를 들어 주머니 속에서 공을 하나 꺼낸 뒤 다시 주머니에 집어넣지 않은 채로 또 다른 공을 하나 더 꺼낸다면 앞서 첫 번째로 공을 꺼낸 사건은 두 번째로 공을 꺼낸 사건에 영향을 준다.
이를 비복원시행이라고 하며 사건 A와 B에 대해 B가 A의 영향을 받는 경우 B는 A의 종속사건이 된다.
✔️ 도박사의 오류
도박사의 오류는 서로 독립적으로 일어나는 확률적 사건이 서로 확률에 영향을 미친다는 착각에서 기인한 오류이다.
만약 주사위를 5번 던져 나온 결과가 2, 4, 3, 5, 1일 때 주사위를 한 번 더 던지면 6이 나올 것 같지만 이는 확신할 수 없다.
매번 주사위를 던질 때마다 6이 나올 확률은 1/6에 해당하며 주사위를 던지는 각 사건은 서로 영향을 주지 않는 독립사건이기 때문이다.
✅ 확률의 연산
✔️ 여사건
여사건은 어떤 사건이 일어나지 않는 경우를 의미한다.
사건 A가 일어나지 않는 경우를 A의 여사건이라 부르며 여사건은 A를 제외한 모든 경우의 수를 포함하므로 다음과 같은 관계가 성립한다.

✔️ 조건부 확률
조건부 확률은 주어진 사건이 일어났다고 가정 하에 다른 한 사건이 일어날 확률을 뜻한다.
사건 B가 일어났다고 가정했을 때 A가 일어날 확률은 다음과 같이 표기한다.

한편, A가 B에 영향을 받지않는 독립사건일 경우 B의 결과와는 상관없이 같은 값을 가지므로 다음의 식이 성립한다.
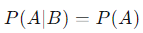
✔️ 곱사건
곱사건은 사건 A와 B가 동시에 일어날 확률을 의미하며 다음과 같이 표기한다.

이때 만약 A가 독립사건이라면 다음이 성립한다.
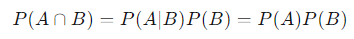
조건부 확률은 곱사건을 이용하여 다음과 같이 계산할 수도 있다.

✔️ 합사건
합사건은 사건 A 또는 B가 일어날 확률을 의미하며 다음과 같이 표기한다.

이때 만약 사건 A와 B의 합사건이 0인 경우 A와 B는 배반사건이라고 하며 다음과 같이 계산할 수 있다.
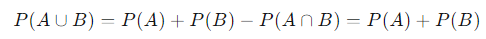
✅ 독립시행
독립시행은 독립사건 A를 여러번 시행하는 것을 의미한다.
한 번의 시행에서 사건 A가 일어날 확률을 p라고 할 때, 이 시행을 n회 반복한 독립시행에서 사건 A가 r번 일어날 확률은 다음과 같다.
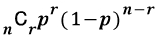
이를 공식으로 정리하면 아래와 같이 표현할 수 있다.
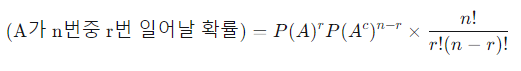
✅ 베이지안 확률론
베이지안 확률론은 주어진 분류 정보를 사용해서 미래에 일어날 확률을 예측하는 확률론을 의미한다.
이는 아래의 공식을 이용한다.
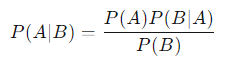
즉, 사건 B가 일어났을 때 사건 A가 일어날 조건부 확률을 다른 정보를 통해 계산하는 것이다.
베이지안 확률론은 주어진 정보만으로 원하는 사건의 확률을 계산할 수 있고 주어진 정보가 충분히 많은 경우 신뢰성이 높아진다.
하지만 주어진 정보가 충분하지 않은 경우에는 결과를 신뢰할 수 없고 처음 보는 사건에 대해서는 확률을 계산하기 어렵다.
🔍 참조
확률 https://ko.wikipedia.org/wiki/%ED%99%95%EB%A5%A0
독립시행 https://m.blog.naver.com/parkhc1992/220562564580
'엘리스 AI 트랙 4기 > Data Analysis Study' 카테고리의 다른 글
| [인공지능/머신러닝 기초] 회귀분석 (0) | 2022.02.13 |
|---|---|
| [인공지능/머신러닝 기초] 선형대수 기초 (0) | 2022.02.12 |
| [프로그래밍수학] 순열과 조합 (0) | 2022.02.10 |
| [프로그래밍수학] 수열 (0) | 2022.02.10 |
| [프로그래밍수학] 소수 (0) | 2022.02.10 |




댓글