엘리스에서 제공한 강의와 자료를 보고 정리한 내용입니다.

✅ 수열
수열은 숫자의 나열을 의미한다.
수열은 나열 순서가 있고 중복이 허용된다는 점에서 집합과 구분된다.
1, 2, 3, 4, 5와 같이 개수가 정해져 있어 끝이 있는 수열을 유한 수열이라고 하며 1, 2, 3, 4, 5, ... 처럼 개수가 정해지지 않아 끝이 없는 수열을 무한 수열이라고 한다.
수열을 이루는 구성원을 수열의 항(term) 또는 원소(element)라고 한다.
수열은 항의 유형에 따라 자연수열, 실수열 등 다양한 형태로 존재할 수 있다.
✔️ 등차수열
등차수열은 연속하는 두 항의 차이가 모두 일정한 수열을 뜻한다.
즉, 일정한 간격으로 원소들이 커지거나 작아진다.
예를 들어 1, 3, 5, 7, 9, ... 는 각 원소들이 2씩 커지고 있기 때문에 등차수열에 해당한다.
이때 두 항의 차이는 수열의 모든 연속하는 두 항들에 대해 공통적으로 나타나는 차이므로 공차(common difference)라고 하며 주로 d로 표시한다.
공차가 양수라면 뒤로 갈수록 수가 커지는 증가 수열이 되며 공차가 음수라면 뒤로 갈수록 수가 작아지는 감소 수열이 된다.
공차가 0이라면 수열의 원소들이 어떤 값을 가지고 있건 상관없이 항상 같은 값을 가지는 수열이 된다.
수열의 첫 항을 a, 공차를 d라고 할 때 등차수열을 나타내는 식은 다음과 같다.
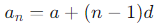
✔️ 등비수열
등비수열은 각 항이 초항과 일정한 비를 가지는 수열을 뜻한다.
등차수열이 일정하게 값이 더해지는 형태라면 등비수열은 일정하게 값이 곱해지는 형태이다.
예를 들어 1, 2, 4, 8, 16, ...은 각 원소들이 2씩 곱해지고 있기 때문에 등비수열에 해당한다.
이때 곱해지는 일정한 상수를 등비(common ratio)라고 부르며 주로 r로 표시한다.
등비수열은 등비의 범위에 따라 다양한 모습을 보인다.
- r > 1 : 곱해질 때마다 수열이 증가하는 형태
- r = 1 : 항상 같은 값을 가지는 형태. 등차수열에서 d=0일 때와 동일.
- 0 < r < 1 : 곱해질 때마다 수열이 감소하는 형태. 0에 가까워지게 됨.
- r = 0 : 첫항을 제외한 모든 값이 0이 됨.
- -1 < r < 0 : 양수, 음수가 번갈아 나타남. 0에 가까워짐.
- r = -1 : 절대값은 같으면서 부호만 번갈아 나타나는 진동수열이 됨. 2개의 값이 반복적으로 나타남.
- r < -1 : 절대값이 계속 커지면서 진동하는 수열이 됨.
수열의 첫 항을 a, 공비를 r이라고 할 때 등비수열을 나타내는 식은 다음과 같다.
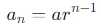
✔️ 계차수열
계차수열은 수열의 인접하는 두 항의 차로 이루어지는 수열이다.
즉, 일정한 규칙을 가진 값들이 더해진다.
예를 들어 수열 1, 4, 9, 16, ... n^2의 계차수열은 3, 5, 7, ..., 2n+1이다.
수열 an의 초항이 a이고 bn을 계차수열로 가지는 수열을 나타내는 식은 다음과 같다.

✔️ 급수
급수는 수열의 모든 항을 더한 것을 의미한다.
해당 수열이 유한수열일 경우 유한급수, 해당 수열이 무한수열일 경우 무한급수로 분류된다.
또 무한급수의 경우 항을 더해가면서 합이 어떤 값에 가까워 지는 수렴급수와 그렇지 않은 발산급수로 나뉜다.
수열의 합을 나타낼 때에는 ∑(시그마) 기호를 사용하며 기호의 아래에는 시작하는 번호를, 위에는 끝나는 번호를 표기하여 범위를 지정한다.

급수를 이용해 계차수열을 표현하면 다음과 같이 나타낼 수 있다.

✔️ 점화식
점화식은 수열에서 이웃하는 두 개의 항 사이에 성립하는 관계를 나타낸다.
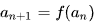
어떠한 수열이 위와 같이 표현된다고 할 때 함수 f를 수열 { an }의 점화식이라고 하며 수열 { an }은 점화식 f로 정의된다고 한다.
일반항과 달리 점화식은 상대적으로 식이 간단하다는 장점이 있으며 일반항으로 나타내기 어려운 수열도 표현할 수 있다.
그러나 n번째의 값을 구하기 위해서는 n-1번째 항의 정보가 필요하기 때문에 초항부터 차근차근 계산해 나가야 한다는 단점이 존재한다.
✅ 수학적 귀납법
수학적 귀납법은 어떠한 등식이 모든 자연수 n에 대해 성립함을 보일 때 주로 쓰이는 증명법이다.
수학적 귀납법의 과정은 다음과 같다.
- 주어진 등식이 n=1일 때 식이 성립함을 보인다.
- 주어진 등식이 n=k일 때 성립한다고 가정했을 때 n=k+1에서도 성립함을 보인다.
- n=1일 때가 성립하므로 (2)에 의해 n=2일때 역시 성립한다.
- n=2일 때가 성립하므로 (2)에 의해 n=3일때 역시 성립한다.
- n=3일 때가 성립하므로 (2)에 의해 n=4일때 역시 성립한다.
… - 따라서 모든 자연수 n에 대해 식이 성립한다.
✏️ 예제 - 수학적 귀납법을 통한 등차수열 합 공식 증명
등차수열의 합 공식은 다음과 같다.

n = 1일 때, 다음과 같이 성립한다.

n = k일 때 성립한다고 가정하고,

n = k + 1일 때를 살펴보면 다음과 같다.

n = k가 성립한다고 가정했을 때 n = k + 1이 성립함을 보였으므로 등차수열의 합 공식은 모든 자연수 n에 대해 성립한다.
🔍 참조
수열 https://ko.wikipedia.org/wiki/%EC%88%98%EC%97%B4
등차수열 https://ko.wikipedia.org/wiki/%EB%93%B1%EC%B0%A8%EC%88%98%EC%97%B4
등비수열 https://ko.wikipedia.org/wiki/%EB%93%B1%EB%B9%84%EC%88%98%EC%97%B4
계차수열 https://ko.wikipedia.org/wiki/%EA%B3%84%EC%B0%A8%EC%88%98%EC%97%B4
점화식 https://ko.wikipedia.org/wiki/%EC%A0%90%ED%99%94%EC%8B%9D
'엘리스 AI 트랙 4기 > Data Analysis Study' 카테고리의 다른 글
| [프로그래밍수학] 확률 (0) | 2022.02.10 |
|---|---|
| [프로그래밍수학] 순열과 조합 (0) | 2022.02.10 |
| [프로그래밍수학] 소수 (0) | 2022.02.10 |
| 머신러닝 종류와 머신러닝 관점 모델 평가 (0) | 2022.02.08 |
| 머신러닝 업무 프로세스와 핵심 용어 (0) | 2022.02.08 |




댓글