문제 링크 >> https://www.acmicpc.net/problem/7453

📋 문제
정수로 이루어진 크기가 같은 배열 A, B, C, D가 있다.
A[a], B[b], C[c], D[d]의 합이 0인 (a, b, c, d) 쌍의 개수를 구하는 프로그램을 작성하시오.
👉 입력
첫째 줄에 배열의 크기 n (1 ≤ n ≤ 4000)이 주어진다.
다음 n개 줄에는 A, B, C, D에 포함되는 정수가 공백으로 구분되어 주어진다.
배열에 들어있는 정수의 절댓값은 최대 228이다.
👈출력
합이 0이 되는 쌍의 개수를 출력한다.
📝 풀이
❌ 첫 번째 풀이
import sys
from itertools import product
input = sys.stdin.readline
n = int(input())
A, B, C, D = [], [], [], []
for _ in range(n):
a, b, c, d = map(int, input().split())
A.append(a)
B.append(b)
C.append(c)
D.append(d)
count = 0
arr = list(product(*[A, B, C, D]))
for item in arr:
if sum(item) == 0:
count += 1
print(count)
첫 번째 풀이는 itertools.product를 이용했다.
네 개의 리스트 A, B, C, D에 각각 해당하는 요소들을 넣고 이들의 조합을 모두 구해 합이 0이 되는 횟수를 출력했다.
그러나 이 풀이는 시간초과가 난다.
itertools.product를 써보고 싶어 A+B만 product로 합을 구해보고 C+D에 이 값에 -1을 곱한 값이 있나 찾아보려 했지만 이 풀이도 시간 초과가 난다.
✔️ 두 번째 풀이
import sys
input = sys.stdin.readline
n = int(input())
A, B, C, D = [], [], [], []
for _ in range(n):
a, b, c, d = map(int, input().split())
A.append(a)
B.append(b)
C.append(c)
D.append(d)
dic = {}
for a in A:
for b in B:
AB = a+b
if AB in dic:
dic[AB] += 1
else:
dic[AB] = 1
count = 0
for c in C:
for d in D:
CD = (c+d) * (-1)
if CD in dic:
count += dic[CD]
print(count)
그래서 두 번째 풀이에서는 딕셔너리를 사용했다.
먼저 A+B를 구한다.
딕셔너리에 key는 A+B, value는 A+B가 등장한 횟수를 저장한다.
그리고 C+D를 살펴본다.
이때 C+D에 -1을 곱한 값이 딕셔너리 dic에 있다면 이는 A+B+C+D = 0이 되는 경우에 해당한다.
따라서 (C+D) * -1이 dic에 있다면 count에 dic[CD]의 value(=A+B가 등장한 횟수)를 더해준다.

✔️ 세 번째 풀이
import sys
input = sys.stdin.readline
n = int(input())
A, B, C, D = [], [], [], []
for _ in range(n):
a, b, c, d = map(int, input().split())
A.append(a)
B.append(b)
C.append(c)
D.append(d)
AB, CD = [], []
for i in range(n):
for j in range(n):
AB.append(A[i] + B[j])
CD.append(C[i] + D[j])
AB.sort()
CD.sort()
start, end = 0, n**2-1
count = 0
while start < len(AB) and end >= 0:
if AB[start] + CD[end] == 0:
count_start, count_end = start + 1, end - 1
while count_start < len(AB) and AB[start] == AB[count_start]:
count_start += 1
while count_end >= 0 and CD[end] == CD[count_end]:
count_end -= 1
count += (count_start - start) * (end - count_end)
start, end = count_start, count_end
elif AB[start] + CD[end] > 0:
end -= 1
else:
start += 1
print(count)
투 포인터로 풀어봤다.
A+B를 AB에 저장하고 C+D를 CD에 저장한다.
그리고 이들을 오름차순으로 정렬한다.
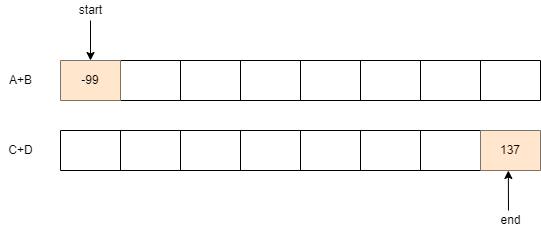
AB를 가리킬 포인터 start는 0으로 초기화해 AB의 첫 번째 요소부터 탐색하고 CD를 가리킬 포인터 end는 n**2-1의 값으로 초기화해 CD의 마지막 요소부터 탐색한다.
이때 n**2-1은 len(CD)-1과 같다.
start가 AB의 끝에 다다르거나 end가 CD의 처음에 다다를 때까지 while문을 순회한다.
그 안에서 AB[start] + CD[end]의 값을 확인한다.
경우의 수는 다음과 같다.
AB[start] + CD[end] > 0 일 경우 AB[start]의 절댓값보다 CD[end]의 값이 크다는 뜻이므로 end의 값을 1 감소시킨다.
AB[start] + CD[end] < 0 일 경우 AB[start]의 절댓값이 CD[end]의 값보다 크다는 뜻이므로 start의 값을 1 증가시킨다.
AB[start] + CD[end] = 0 일 경우에는 현재 AB[start]와 CD[end]의 동일한 값이 AB와 CD에 존재하는지 확인해야 한다.
만약 현재 값과 같은 값이 있을 경우 그것도 합이 0이 되는 경우이기 때문이다.
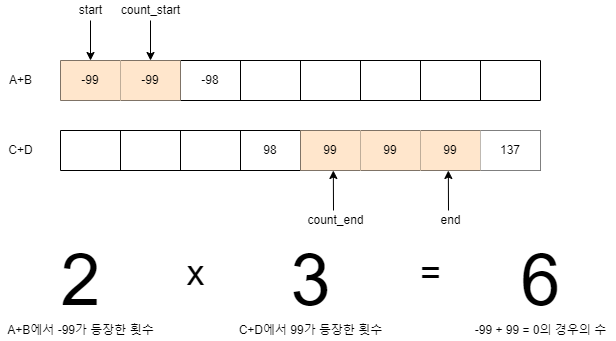
따라서 start + 1을 count_start에, end - 1을 count_end에 저장해둔다.
그리고 while문 안에서 start와 end가 각각 해당하는 범위 내에 있는지, AB[start] 또는 CD[end]와 동일한 값이 존재하는지 확인한 후 같은 값이 등장한 횟수를 센다.
그리고 합이 0이 되는 횟수를 저장할 변수 count에 (AB[start]와 동일한 값이 등장한 횟수) * (CD[end]와 동일한 값이 등장한 횟수)를 더해준다.

두 번째 풀이보다 메모리나 시간이나 모두 줄어든 것을 확인할 수 있다.
'Algorithm > Python' 카테고리의 다른 글
| [프로그래머스] 카펫 (0) | 2022.03.05 |
|---|---|
| [프로그래머스] 더 맵게 (0) | 2022.03.04 |
| [백준 2470번] 두 용액 (0) | 2022.03.02 |
| [프로그래머스] 소수 찾기 (0) | 2022.03.02 |
| [백준 17609번] 회문 (0) | 2022.03.01 |




댓글